Introduction

In a previous life, I wrote a Sudoku solver that relied on Poetry's dependency resolver. We ended up selling that startup to EDB (not because of the Poetry hack), which means that they now own this IP. And, since then, Python packaging has advanced, with uv taking the world by storm.

This means that it's time for a refresh. Can we use uv instead of Poetry? And can we solve a Wordle instead of a Sudoku?

For the impatient: you can get the solver from my GitHub. Run uv run main.py run and watch it go.

Background: Sudoku and Python dependency resolution

The short summary of the Sudoku + Poetry post is that unlike Rust or JavaScript, a single Python project cannot use more than one version of a specific Python package. This means that we can easily represent a Sudoku grid as 81 Python packages, each with 9 possible versions. If a certain cell has a specific number (version), cells in the same row, column and a 3x3 square it belongs to cannot have that same number.

We can encode these rules as version constraints on other packages representing our cell's neighbours.

Once we have our 81 packages, all that remains is encoding our problem by making another package, specifying the precise versions of the cells where we already have numbers, leaving the rest as wildcards, and then letting Poetry generate a lockfile that will assign each number (version) to every cell (package), thus solving the puzzle.

What is Wordle

This is Wordle.

You have six attempts to guess a five-letter word. On each guess, you get what I'll be calling "feedback": each letter in your guess becomes green (correct letter in the correct position), yellow (correct letter, wrong position) or nothing (wrong letter).

In this post, I'll represent it as a string YGG.., meaning that the feedback we got for our answer is:

• Yellow at position 1
• Green at positions 2 and 3
• Blank or "dot" at positions 4 and 5

Analysis

It is said that if you ask an LLM to think really hard about its answer and write down its thinking before giving the final response, then it can successfully count the number of r's in the word strawberrry and help you sell more inference tokens.

Let's do exactly that and break this down.

Basic building blocks

Let's start simple. The solution to a Wordle is a five-letter word, and we'd like our system to choose one possible word given all information that we feed into it. We can encode this as a single Python package with multiple possible versions, where each version represents a single word. This is a useful building block.

The other building block is that each position can only have one letter in it. We can easily represent this as five "position" packages, each of which can have 26 versions. If the position package 1 has version 2, that means "B" is in that position.

We can then draw dependencies between a specific version of our "word" package to specific versions of our "position" packages. If our word is STALL, then it'll depend on:

• position package 1, version 19 (S)
• position package 2, version 20 (T)
• position package 3, version 1 (A)
• position packages 4 and 5, version 12 (L)

Greens and yellows

However, this is not enough. We need to encode some more complex facts about the solution in Wordle than we did with Sudoku. For example, let's assume that we guessed CHILD and the feedback we got is ..YG.. This means:

• The fourth letter is L
• The third letter is not I
• But there is at least one I somewhere in the word
• None of the letters are C, H or D

Is this correct though? There is a bit of nuance here.

Let's try again, this time with a different guess but the same word. We try ATOLL (it's not an optimal play, but as a demonstration) and get ...GY. Here, we can't just say that there is an L somewhere in the word (because there already is). We have to say that there is at least one L in the first, second or third position.

Now let's say we guess LILLE and get .GGG.. What does this mean? Just because L in the first position gave us a dot doesn't mean there are no Ls in the word at all (there clearly are). Instead, we need to say that the first and the fifth position don't contain an L.

One thing that stems from this is that the feedback we get for a specific letter in a specific position will change based on other letters in our guess. For example, let's say the real world is BUNNY. If we guess NNNON, we'll get YYG.Y. And if we then guess NNNNN, we'll get ..GG.. Because we discovered all Ns in the word, the first, second and last letters become blanks instead of yellows.

So, these are the inferences we can draw when given a guess and the feedback:

• If a letter in a certain position is green: that letter has to be in that position
• If it's yellow: then the letter is not in that position and at least one of the positions that are not green have to have that letter
• If it's blank: none of the positions that aren't green or yellow have that letter

Python dependency rules?

However, encoding this as Python dependency rules isn't going to be fun. Because the feedback for a specific letter in a specific position can change, we can't have a fact like "N in position 3 is blank": we have to preprocess the feedback and somehow encode these basic facts about which letters can or can't be in specific positions.

Python also doesn't support a package depending on one of several other packages. That is, if I want to encode that at least one of positions 1, 2 or 3 contains the letter L, I can't say "My package depends on either position package 1, version 12, or position package 2, version 12, or position package 3, version 12".

Possible position packages

Instead, the encoding scheme I came up with is as follows. Let's add another set of packages, one for each letter. The version selected for this package will represent what positions this letter we think can appear in. So, in the above ATOLL / ...GY example, we will say that we can select versions [1,4], [2,4], [3,4], [1,2,4], [1,3,4], [1,2,3,4] of the possible position package for L, i.e. all versions where L appears at position 4, doesn't appear in position 5 and appears in at least one position of 1, 2, or 3.

Each possible position package has 32 versions, and we can use binary encoding to turn each list of possible positions into an allowed version ([1, 4]would get encoded as binary 10010, that is, 18, and so on).

Feedback packages

We could produce version constraints on possible position packages directly from the feedback we get for our guesses, but that would be doing too much work outside of uv.

Let's introduce another set of packages and call them "feedback packages". Each one will represent a statement like "L is in at least one of positions 1, 2, 3" and will have two versions: 0 (meaning False, i.e. L is in neither of 1, 2 or 3) or 1 (meaning True). Then, encoding the feedback we got for our guess is a matter of adding dependencies on feedback packages to our project:

• If a letter in a certain position is green: add a dependency on {letter}_in_{position}, version 1
• If it's yellow:
  • add a dependency on {letter}_in_{position} version 0 for that position
  • let other_positions be all positions that aren't green and aren't position itself, add a dependency on {letter}_in_{other_positions}, version 1
• If it's blank: let positions be all positions that aren't green or yellow, add a dependency on {letter}_in_{positions}, version 0

Putting this all together: the cursed neural network

Let's connect all these sets of packages with dependency rules:

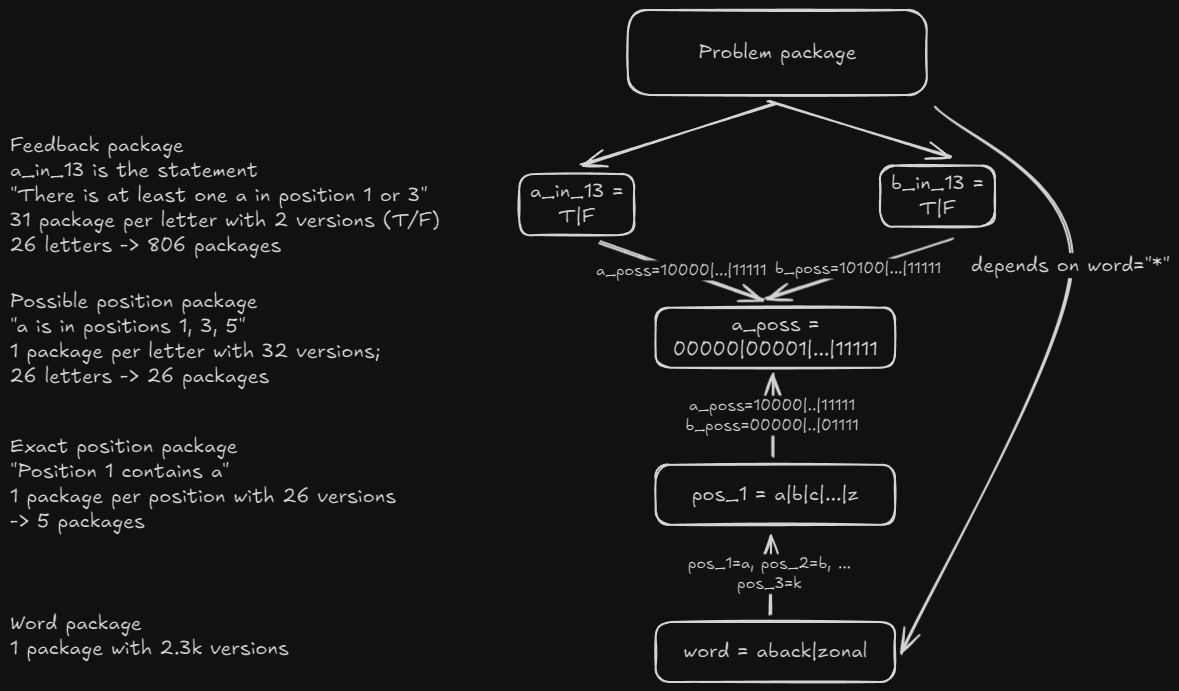
We have our "input layer", which is our feedback packages. Those depend on our "hidden layer" packages, or possible position packages, using straightforward rules. Version 1 of a_in_13 depends on any version of a_poss that has 1 or 3 checked, and version 0 of a_in_13 depends on any version of a_poss that doesn't have neither 1 or 3 checked.

On the other side, we have our "exact position" packages that also depend on the possible position packages. If position 1 has A (pos_1 has version 1), that means that it depends on all versions of a_poss that have A in position 1. Crucially, it also depends on the versions of all other possible position packages (representing other letters) that don't have that letter in position 1. That is, if we have A in position 1, we better exclude all solutions that have B in position 1.

Finally, we have a couple thousand versions of the word package. Each one represents a potential solution and enforces the exact letters in each position via position packages.

And finally finally, our "problem" package has a dependency on any version of the word package and the feedback packages which we will dynamically add to the dependency list as we make guesses and get feedback from Wordle.

Implementation

I wasn't going to make 5,000 package versions myself, so I wrote a Python program to generate them all.

Package examples

Here's a sample feedback package with dependencies on a possible positions package:

[project]
name = "wordle_a_in_125"
version = "1"
dependencies = [ "wordle_a_poss !=0,!=2,!=4,!=6",]

[build-system]
requires = [ "uv_build>=0.7.19,<0.8.0",]
build-backend = "uv_build"

You'll notice something interesting here. I couldn't find a way to make a package depend on one of a certain list of versions in the Python dependency specifier guide, so instead I inverted the dependency specification. If I have a list of possible versions, I could also say "this package can't depend on any version that isn't in my list" and enumerate those versions.

Its inverse (version 0) has the opposite set of packages:

[project]
name = "wordle_a_in_125"
version = "0"
dependencies = [ "wordle_a_poss !=1,!=3,!=5,!=7,!=8,!=9,!=10,!=11,!=12,!=13,!=14,!=15,!=16,!=17,!=18,!=19,!=20,!=21,!=22,!=23,!=24,!=25,!=26,!=27,!=28,!=29,!=30,!=31",]

[build-system]
requires = [ "uv_build>=0.7.19,<0.8.0",]
build-backend = "uv_build"

A possible positions package doesn't have any dependencies:

[project]
name = "wordle_a_poss"
version = "5"

[build-system]
requires = [ "uv_build>=0.7.19,<0.8.0",]
build-backend = "uv_build"

An exact position package for the statement "A is in position 1" constrains the possible positions package for A to have that letter in position 1 and for other letters to not have them in that position:

[project]
name = "wordle_pos_1"
version = "1"
dependencies = [ "wordle_a_poss !=0,!=1,!=2,!=3,!=4,!=5,!=6,!=7,!=8,!=9,!=10,!=11,!=12,!=13,!=14,!=15", "wordle_b_poss !=16,!=17,!=18,!=19,!=20,!=21,!=22,!=23,!=24,!=25,!=26,!=27,!=28,!=29,!=30,!=31", "wordle_c_poss ..."]

[build-system]
requires = [ "uv_build>=0.7.19,<0.8.0",]
build-backend = "uv_build"

Here's the definition for the word package version 58, representing the word "ALLOY" (I got the wordlist here):

[project]
name = "wordle_word"
version = "58"
dependencies = [ "wordle_pos_1 ==1", "wordle_pos_2 ==12", "wordle_pos_3 ==12", "wordle_pos_4 ==15", "wordle_pos_5 ==25",]

[build-system]
requires = [ "uv_build>=0.7.19,<0.8.0",]
build-backend = "uv_build"

--find-links and wheels

Instead of using a devpi instance like I did with the Poetry solver, I managed to make uv output wheels to a single directory (hence the build-system stanza in every package). Then, I could use uv lock --find-links ../output/wheels, which would execute uv's dependency resolver directly against this directory, without having to run a local registry.

uv is really fast. Building 4,883 wheels took only 2 minutes on my machine: that's about 40 wheels a second!

Harness

Given all this, I wrote a simple harness that, in a loop:

• Gets the feedback for a guess
• Generates a pyproject.toml file for a "problem" package, turning the feedback into a set of constraints on the "feedback" packages (appending to existing constraints from previous attempts)
• Executes uv lock
• Reads the version of the word package that uv chose and attempts that as a guess
• If the dependency resolution failed, there is no solution to the Wordle in our wordlist.

Here is a sample pyproject.toml file after a few loops:

[project]
name = "problem"
version = "0.1.0"
dependencies = [ "wordle_word", "wordle_b_in_12345 ==0", "wordle_o_in_12345 ==0", "wordle_b_in_12345 ==0", "wordle_b_in_12345 ==0", "wordle_y_in_12345 ==0", "wordle_w_in_12345 ==0", "wordle_r_in_12345 ==0", "wordle_u_in_12345 ==0", "wordle_n_in_12345 ==0", "wordle_g_in_12345 ==0", "wordle_v_in_12345 ==0", "wordle_i_in_12345 ==0", "wordle_v_in_12345 ==0", "wordle_i_in_12345 ==0", "wordle_d_in_12345 ==0", "wordle_t_in_1 ==0", "wordle_t_in_2345 ==1", "wordle_t_in_4 ==0", "wordle_t_in_1235 ==1", "wordle_a_in_5 ==0", "wordle_a_in_1234 ==1", "wordle_h_in_23 ==0", "wordle_e_in_23 ==0",]

Bonus round: more efficient guessing

One final thing: there are plenty of Wordle strategies out there and we can employ them to make our solver more clever.

uv tries to select the newest version of a package, which means that we can sort our wordlist so that the more preferable words have a bigger version number.

I defined a simple sorting order: we prefer words that have more distinct characters, and then the ones where the characters are the most frequent:

_FREQUENCIES: Counter = Counter()

for word in WORDS:
    _FREQUENCIES.update(word)


def _score(word):
    """Custom scoring function for guesses: we prioritize words with as many
    distinct characters as possible, and then the ones with the most frequent
    letters"""

    no_distinct = len(set(word))
    freq_score = sum(_FREQUENCIES[c] for c in word)
    return (no_distinct, freq_score)


WORDS = sorted(WORDS, key=_score)

This means that the first guess it attempts is "LATER".

Blooper reel

By accident, at first, I omitted the letter u in my list of letters that I was generating packages for, which caused extremely cryptic and long (500KB of uv painstakingly explaining to me why I was wrong) dependency resolution errors on specific guesses:

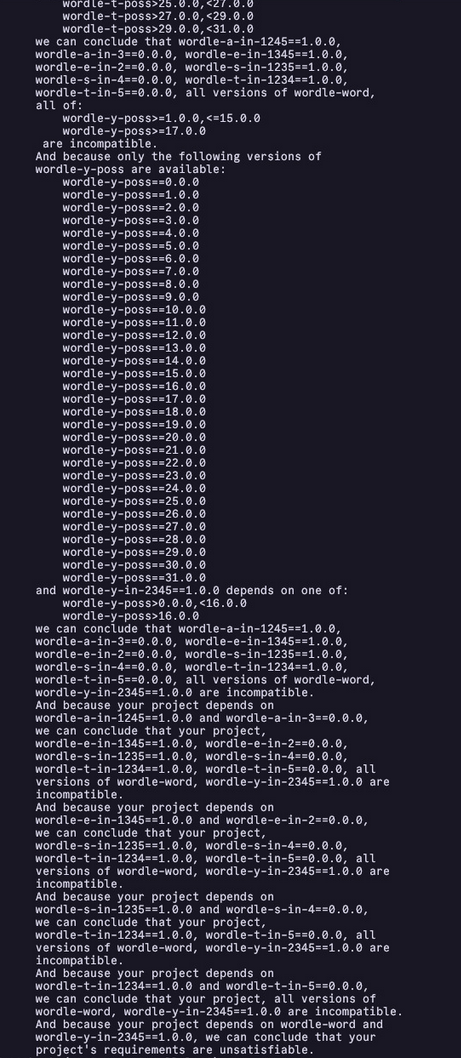
I found a neat trick to debug these, in case anyone ever gets stuck turning uv into a SAT solver and needs help. I pinned my word dependency to the exact word that I had in mind and got a very short error message saying that the pos_2 package version 21 (representing U) didn't exist.

GitHub

The source code for this beautiful work of art is on my GitHub. You just need uv itself and you can execute the solver as follows:

uv run main.py run 

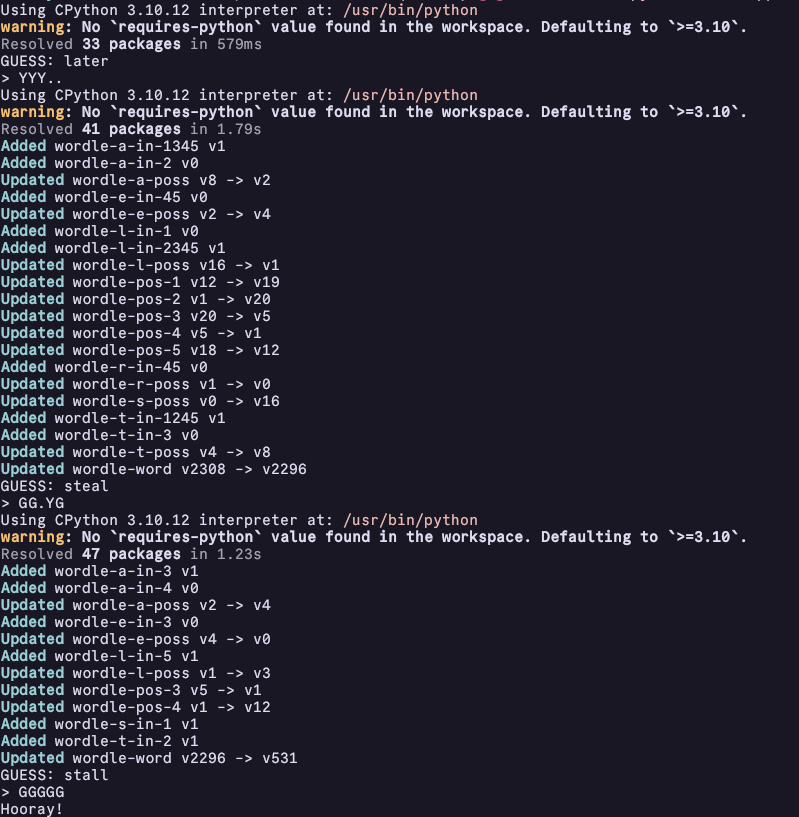
It'll generate the constraint packages and drop you into a solver loop. You can even pass --no-suppress to watch uv do its magic:

uv run main.py run --no-suppress --no-emit-project
Using CPython 3.10.12 interpreter at: /usr/bin/python
warning: No `requires-python` value found in the workspace. Defaulting to `>=3.10`.
Resolved 33 packages in 579ms
GUESS: later
> YYY..
Using CPython 3.10.12 interpreter at: /usr/bin/python
warning: No `requires-python` value found in the workspace. Defaulting to `>=3.10`.
Resolved 41 packages in 1.79s
Added wordle-a-in-1345 v1
Added wordle-a-in-2 v0
Updated wordle-a-poss v8 -> v2
Added wordle-e-in-45 v0
Updated wordle-e-poss v2 -> v4
Added wordle-l-in-1 v0
Added wordle-l-in-2345 v1
Updated wordle-l-poss v16 -> v1
Updated wordle-pos-1 v12 -> v19
Updated wordle-pos-2 v1 -> v20
Updated wordle-pos-3 v20 -> v5
Updated wordle-pos-4 v5 -> v1
Updated wordle-pos-5 v18 -> v12
Added wordle-r-in-45 v0
Updated wordle-r-poss v1 -> v0
Updated wordle-s-poss v0 -> v16
Added wordle-t-in-1245 v1
Added wordle-t-in-3 v0
Updated wordle-t-poss v4 -> v8
Updated wordle-word v2308 -> v2296
GUESS: steal
> GG.YG
Using CPython 3.10.12 interpreter at: /usr/bin/python
warning: No `requires-python` value found in the workspace. Defaulting to `>=3.10`.
Resolved 47 packages in 1.23s
Added wordle-a-in-3 v1
Added wordle-a-in-4 v0
Updated wordle-a-poss v2 -> v4
Added wordle-e-in-3 v0
Updated wordle-e-poss v4 -> v0
Added wordle-l-in-5 v1
Updated wordle-l-poss v1 -> v3
Updated wordle-pos-3 v5 -> v1
Updated wordle-pos-4 v1 -> v12
Added wordle-s-in-1 v1
Added wordle-t-in-2 v1
Updated wordle-word v2296 -> v531
GUESS: stall
> GGGGG
Hooray!